最近、Google Discoverがやたらと「19×19までの掛け算を暗算する方法」に関する記事をオススメしてきます。(私がそういうページを見た結果だと思うのですが。)
記事を読んでみるのですが「おみやげ算」と呼ばれる謎の理論が展開されており、次の日になったら忘れそうな内容のため(実際には最後まで読まずに諦めるのですが)、暗算ができるようなった気がしません。
というわけで、自分で暗算できるように考えてみました。
19×19までの掛け算を暗算する手順(R2F版)
2つの数の1の位の数字について、一方を\(a\in(1,2,\ldots,9)\)、もう一方を\(b\in(1,2,\ldots,9)\)とすると、式は次の通りとなります。
\((10+a)\times(10+b)\)
図で考える
掛け算を長方形の面積に置き換えて考えます。
縦の長さが(10+a)、横の長さが(10+b)の長方形を次のように図にします。
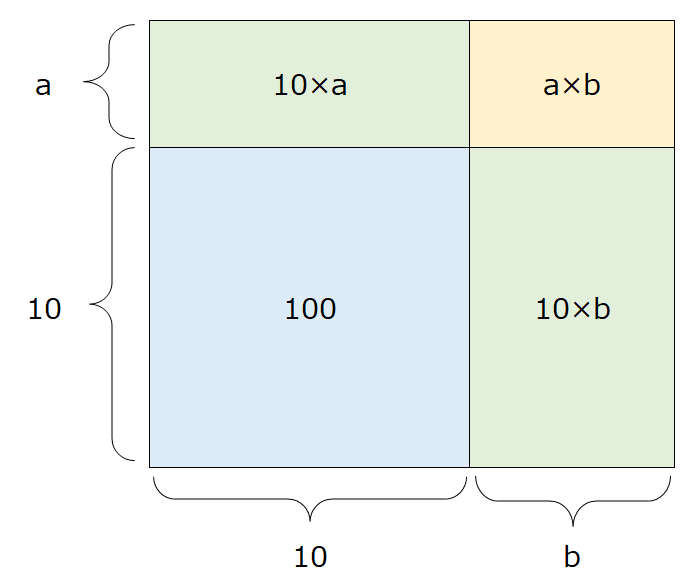
長方形の面積=青い部分の面積+緑の部分の面積+黄色の部分の面積、と分けて考えると次のように変換できます。

緑の長方形が2個ありますが、片方の辺の長さが10なので、さらに次のように変換します。

ここまで来れば、あとはa+bとa×bが分かれば計算できそうです。例えば16×18を計算する場合は、a=6、b=8とするとa+b=14、a×b=48なります。
青の部分は十の位が1同士の掛け算の場合は必ず100になるので、計算は緑、青、黄色の順に、下記の青色の筆算を頭の中でイメージすればなんとか暗算できるのではないかと思います。

これで伝わったでしょうか?
11×11~19×19まで計算してみる
ここまで説明した方法で、11×11から19×19の全81パターンの計算をしてみます。
11の段の計算
11×11

11×12

11×13

11×14

11×15

11×16

11×17

11×18

11×19

12の段の計算
12×11

12×12

12×13

12×14

12×15

12×16

12×17

12×18

12×19

13の段の計算
13×11

13×12

13×13

13×14

13×15

13×16

13×17

13×18

13×19

14の段の計算
14×11

14×12

14×13

14×14

14×15

14×16

14×17

14×18

14×19

15の段の計算
15×11

15×12

15×13

15×14

15×15

15×16

15×17

15×18

15×19

16の段の計算
16×11

16×12

16×13

16×14

16×15

16×16

16×17

16×18

16×19

17の段の計算
17×11

17×12

17×13

17×14

17×15

17×16

17×17

17×18

17×19

18の段の計算
18×11

18×12

18×13

18×14

18×15

18×16

18×17

18×18

18×19

19の段の計算
19×11

19×12

19×13

19×14

19×15

19×16

19×17

19×18

19×19

計算してみて
数秒あれば計算できなくはないのですが、イマイチしっくりこないところもあります。
全81パターン(11×11、、、19×19)ではないですが、特定のパターンについては別の方法でもっと速く計算できていたので、その辺りをもう少し体系的に整理して続編を書こうと思います。

