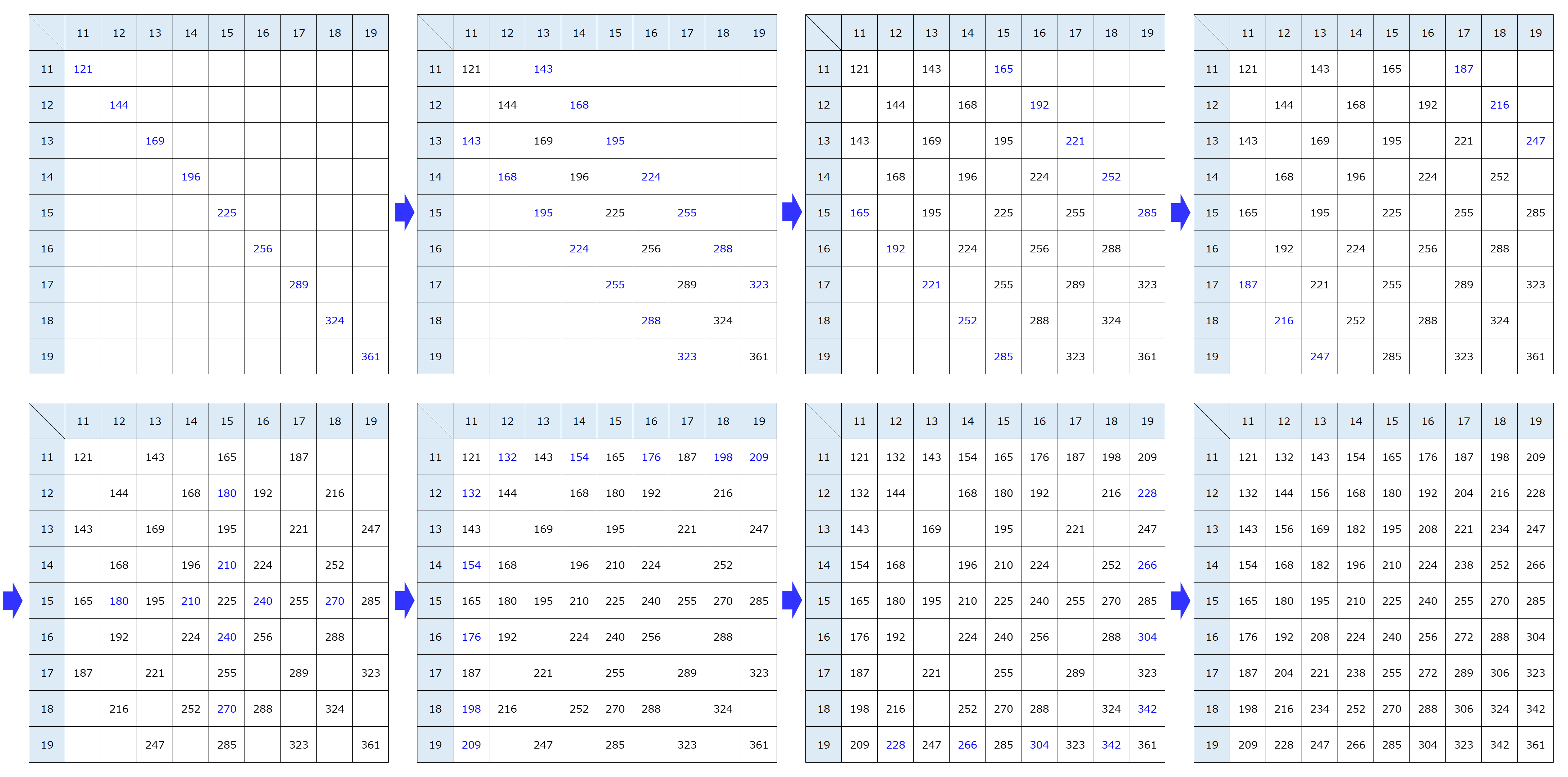
前回に提案した方法より速く暗算できる方法を整理してみました。
前回の記事はこちらから確認ください。
19×19までの掛け算を暗算する手順(R2F版ver.2)
一部暗記を含みますが、半分くらいの組合せについては前回の方法より速く正確に暗算できそうです。
step1:\(n^{2}\)を暗記する
計算でよく使う掛け算は暗記してしまいます。
- 11×11=121
- 12×12=144
- 13×13=169
- 14×14=196
- 15×15=225
- 16×16=256
- 17×17=289
- 18×18=324
- 19×19=361
2次方程式や3平方の定義を利用した問題を解く際に(掛け算ではなく、平方根の計算で)よく登場する数字なので覚えて損はありません。私は中学生のときに15×15まで、高校生のときに25×25まで覚えてました。覚えていたおかげで計算時間の短縮に繋がりました。
完璧に覚えていなくてもだいたいこれくらいの数字だというのが肌間隔として身についてくれば、例えば18×18の答えが思い出せなくても「18×18は17×17=289より大きくて、19×19=361より小さくて、確か320くらいだったから、8×8=64だから18×18の計算結果の1の位も4で、、、答えは324だったはずだ。間違いない。」と、慣れれば思い出せるようになります。
これを覚えると、全81パターンのうち9パターンが一瞬で暗算できます。正確には覚えてるので暗算では無いかもしれませんが。

ここまでで、カバレッジとしては9/81=11.1%となります。
step2:(n+1)(n-1)=\(n^{2}\)-1を活用する
先ほどのn2を暗記する方法の延長線ですが、2つの数字の差が2である場合に威力を発揮します。
例えば18×16を計算する場合、
18×16
=(17+1)(17-1)
=172-12
として、172=289を覚えていれば、続きを
=289-1
=288
とスラスラと計算できます。暗記しているn2から1引くだけなので、体感的には1秒以内で暗算できると思います。

青字で書いた箇所が追加で暗算できるようになりました。
ここまでで、カバレッジとしては23/81=28.3%となります。
これだけで11×11から19×19までの計算の4分の1以上が瞬殺できるようになりました。
step3:(n+2)(n-2)=\(n^{2}\)-4を活用する
step2と考え方は同じです。2つの数字の差が4である場合に、真ん中の数をnとすると、n2-4が答えになります。
例えば13×17を計算する場合、
13×17
=(15-2)(15+2)
=152-22
として、152=225を覚えていれば、続きを
=225-4
=221
とスラスラと計算できます。暗記しているn2から4引くだけなので、繰り下がりもないことから体感的には1秒以内で暗算できると思います。

青字で書いた箇所が追加で暗算できるようになりました。
ここまでで、カバレッジとしては33/81=40.7%となります。
これだけで11×11から19×19までの計算の40%以上が暗算できるようになりました。
step4:(n+3)(n-3)=\(n^{2}\)-9を活用する
step2、step3と考え方は同じです。2つの数字の差が6である場合に、真ん中の数をnとすると、n2-9が答えになります。
例えば19×13を計算する場合、
19×13
=(16+3)(16-3)
=162-32
として、162=256を覚えていれば、続きを
=256-9
=247
とスラスラと計算できます。暗記しているn2から9引くだけなのですが、1の位の繰り下げりの計算が発生するので、これまでより少し時間が増えて暗算に2~3秒くらい掛かるかもしれませんが、前回の記事で書いた計算方法よりは速く暗算できると思います。

青字で書いた箇所が追加で暗算できるようになりました。
ここまでで、カバレッジとしては39/81=48.1%となります。
step5:15の段を暗算する
掛け算九九を覚えるのに最初に1の段、2の段、5の段を覚えると思いますが、5の段は簡単だ→15の段もまあまあ簡単に違いない、という少し強引な理論で暗算します。
ここまで紹介した方法で計算ができないパターンは次の4つで、全て15×偶数です。
- 15×12
- 15×14
- 15×16
- 15×18
例えば15×12を計算しようと思うと、
15×12
=12×15
=12×1.5×10
=18×10
=180
と計算できます。具体的には12の1.5倍が計算できればよくて、偶数の1.5倍なので
12×1.5
=12×1+12×0.5
=12+6
=18
が暗算できれば計算できます。
同様に、
15×14
=14×15
=14×1.5×10
=21×10
=210
15×16
=16×15
=16×1.5×10
=24×10
=240
15×18
=18×15
=18×1.5×10
=27×10
=270
と暗算できます。

これで青字で書いた箇所が追加で暗算できるようになりました。
ここまでで、カバレッジとしては47/81=58.0%となります。
ついに11×11から19×19までの計算の半分以上が暗算できるようになりました。
step6:11の段を暗算する
step5と同様に、1の段は簡単だ→11の段もまあまあ簡単なはずだ、という理論で暗算します。
ここまで紹介した方法で計算ができないパターンは次の5つです。
- 11×12
- 11×14
- 11×16
- 11×18
- 11×19
例えば11×18を計算しようと思うと、
11×18
=18×11
=18×(10+1)
=18×10+18×1
=180+18
=198
と計算します。18×11を筆算するイメージを考えれば暗算できます。

この図の青字の部分だけを頭の中でイメージして計算します。19×11以外は繰り上がりも無いので簡単です。
同様に、
11×12
=12×11
=120+12
=132
11×14
=14×11
=140+14
=154
11×16
=16×11
=160+16
=176
11×19
=19×11
=190+19
=209
と暗算できます。
11の段は全てこの方法で良いかもしれません。

これで青字で書いた箇所が追加で暗算できるようになりました。
ここまでで、カバレッジとしては57/81=70.3%となります。
step7:19の段を暗算する
step6では11段の計算をする際に、もう1個の数の10倍と1倍を足す考え方としましたが、19の段の計算では、もう1個の数の20倍から1倍を引くと考えます。
ここまで紹介した方法で計算ができないパターンは次の4つです。
- 19×12
- 19×14
- 19×16
- 19×18
例えば19×16を計算しようと思うと、
19×16
=16×19
=16×(20-1)
=16×20-16×1
=320-16
=304
と計算します。
同様に、
19×12
=12×19
=240-12
=228
19×14
=14×19
=280-14
=266
19×18
=18×19
=360-18
=342
と暗算できます。

これで青字で書いた箇所が追加で暗算できるようになりました。
ここまでで、カバレッジとしては65/81=80.2%となります。
step8:前回の方法で計算
残ったパターンについては、これといった方法が無く、私もこれまで暗算できなかったので前回紹介した方法で計算して下さい。(笑)
残ったのは次の16パターンです。
- 12×13
- 12×17
- 13×12
- 13×14
- 13×16
- 13×18
- 14×13
- 14×17
- 16×13
- 16×17
- 17×12
- 17×14
- 17×16
- 17×18
- 18×13
- 18×17
全部、計算します。
- 12×13 → 2+3=5、5×10=50、50+100=150、150+2×3=150+6=156
- 12×17 → 2+7=9、9×10=90、90+100=190、190+2×7=190+14=204
- 13×12 → 3+2=5、5×10=50、50+100=150、150+3×2=150+6=156
- 13×14 → 3+4=7、7×10=70、70+100=170、170+3×4=170+12=182
- 13×16 → 3+6=9、9×10=90、90+100=190、190+3×6=190+18=208
- 13×18 → 3+8=11、11×10=110、110+100=210、210+3×8=210+24=234
- 14×13 → 4+3=7、7×10=70、70+100=170、170+4×3=170+12=182
- 14×17 → 4+7=11、11×10=110、110+100=210、210+4×7=210+28=238
- 16×13 → 6+3=9、9×10=90、90+100=190、190+6×3=190+18=208
- 16×17 → 6+7=13、13×10=130、130+100=230、230+6×7=230+42=272
- 17×12 → 7+2=9、9×10=90、90+100=190、190+7×2=190+14=204
- 17×14 → 7+4=11、11×10=110、110+100=210、210+7×4=210+28=238
- 17×16 → 7+6=13、13×10=130、130+100=230、230+7×6=230+42=272
- 17×18 → 7+8=15、15×10=150、150+100=250、250+7×8=250+56=306
- 18×13 → 8+3=11、11×10=110、110+100=210、210+8×3=210+24=234
- 18×17 → 8+7=15、15×10=150、150+100=250、250+8×7=250+56=306

無事に、全部暗算できました。
計算してみて
速ければいいというものではありませんが、ここで紹介したstep7までの方法を使うことで、step7までの80%くらいについては前回より速く暗算することができました。
| step | 計算パターン | パターン数 | 累計パターン数 | 今回の方法 | 前回の方法 |
| 1 | n×n | 9 | 9(11.1%) | 1秒以内 | 5秒くらい |
| 2 | (n+1)(n-1) | 14 | 23(28.3%) | 1秒以内 | 5秒くらい |
| 3 | (n+2)(n-2) | 10 | 33(40.7%) | 1秒以内 | 5秒くらい |
| 4 | (n+3)(n-3) | 6 | 39(48.1%) | 3秒以内 | 5秒くらい |
| 5 | 15×n | 8 | 47(58%) | 3秒以内 | 5秒くらい |
| 6 | 11×n | 10 | 57(70.3%) | 3秒以内 | 5秒くらい |
| 7 | 19×n | 8 | 65(80.2%) | 3秒以内 | 5秒くらい |
| 8 | その他 | 16 | 81(100%) | 5秒くらい | 5秒くらい |